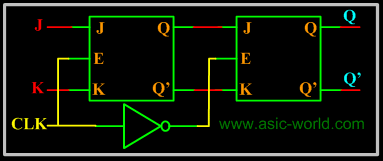
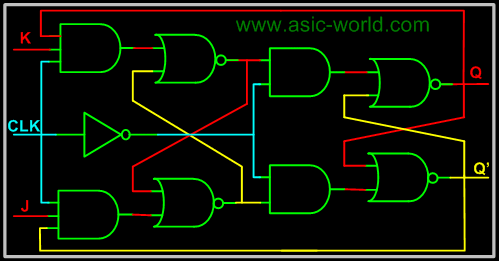
K Master Slave Flip-Flop
All sequential circuits that we have seen in the last few pages have a problem (All level sensitive sequential circuits have this problem).
Before the enable input changes state from HIGH to LOW (assuming HIGH is ON and LOW is OFF state), if inputs changes, then another state transition occurs for the same enable pulse. This sort of multiple transition problem is called racing.
If we make the sequential element sensitive to edges, instead of levels, we can overcome this problem, as input is evaluated only during enable/clock edges.

In the figure above there are two latches, the first latch on the left is called master latch and the one on the right is called slave latch. Master latch is positively clocked and slave latch is negatively clocked
Sequential Circuits Design
We saw in the combinational circuits section how to design a combinational circuit from the given problem. We convert the problem into a truth table, then draw K-map for the truth table, and then finally draw the gate level circuit for the problem. Similarly we have a flow for the sequential circuit design. The steps are given below.
Draw state diagram.
Draw the state table (excitation table) for each output.
Draw the K-map for each output.
Draw the circuit.
Looks like sequential circuit design flow is very much the same as for combinational circuit.
State Diagram
The state diagram is constructed using all the states of the sequential circuit in question. It builds up the relationship between various states and also shows how inputs affect the states.
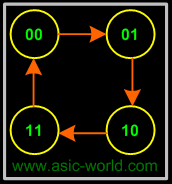
To ease the following of the tutorial, let's consider designing the 2 bit up counter (Binary counter is one which counts a binary sequence) using the T flip-flop
Below is the state diagram of the 2-bit binary counter.
State Table
The state table is the same as the excitation table of a flip-flop, i.e. what inputs need to be applied to get the required output. In other words this table gives the inputs required to produce the specific outputs.
|
|
K-map
The K-map is the same as the combinational circuits K-map. Only difference: we draw K-map for the inputs i.e. T1 and T0 in the above table. From the table we deduct that we don't need to draw K-map for T0, as it is high for all the state combinations. But for T1 we need to draw the K-map as shown below, using SOP.
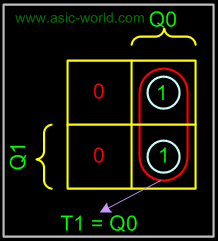
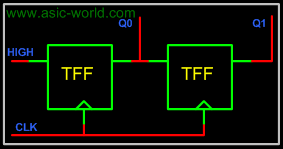
Circuit
There is nothing special in drawing the circuit, it is the same as any circuit drawing from K-map output. Below is the circuit of 2-bit up counter using the T flip-flop.
Bạn Có Đam Mê Với Vi Mạch hay Nhúng - Bạn Muốn Trau Dồi Thêm Kĩ Năng
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn